Most of you may not know this but gamblers, who called upon mathematicians to provide optimal winning strategies, lead the early development of probability & combinatorics. Since then, probability theory has expanded beyond gambling. Now it has vast applications in many fields such as politics, business, etc. and of course GRE!
My emphasis in writing this GRE probability tutorial is to help you understand the GRE probability concepts tested on the GRE exam. Of course, Probability is a very large topic but GRE only tests specific topics on Probability. Therefore the purpose of this post is not just to discuss the GRE probability formulas and rules. But it will also provide clarity and conceptual understanding of GRE level probability. I have tried to demonstrate the GRE probability concepts via specific GRE type example questions.
So let’s start.
In this Article
1. Definitions
Observation
Any recording of information, whether numerical or categorical, is an observation. For example, R, N, R, R, N, N, and R (categorical data) represents days with rain (R) or without rain (N) in a 7-day week. Here R and N are observations. Similarly, the numbers 1, 2, 2, and 3 (numerical data) represents the number of times various students have taken the GRE. Here 1, 2 and 3 are the recorded observations.
Experiment
GRE uses the word experiment to describe any procedure that generates a set of data. For example rolling a dice once is an experiment. In this experiment, there are only six possible outcomes, 1 through 6. Another example of an experiment is rolling a coin twice. In this experiment, there are 4 possible outcomes, HH, HT, TH, and TT – where H and T correspond to heads and tails, respectively.
Sample Space
The set of all possible outcomes of an experiment is called the sample space and is generally represented by the symbol S. But GRE can represent it using some other variable as well.
Each outcome in a sample space is called an element. Thus, the sample space S, of possible outcomes when a coin is flipped twice, may be written
S = {HH, TT, HT, TH}, where H and T correspond to heads and tails, respectively and HH, TT, HT, TH, each is an element of the sample space.
Consider the experiment of tossing a die. In this case, the sample space is
S = {1, 2, 3, 4, 5, 6} where each number 1 till 6 is an element.
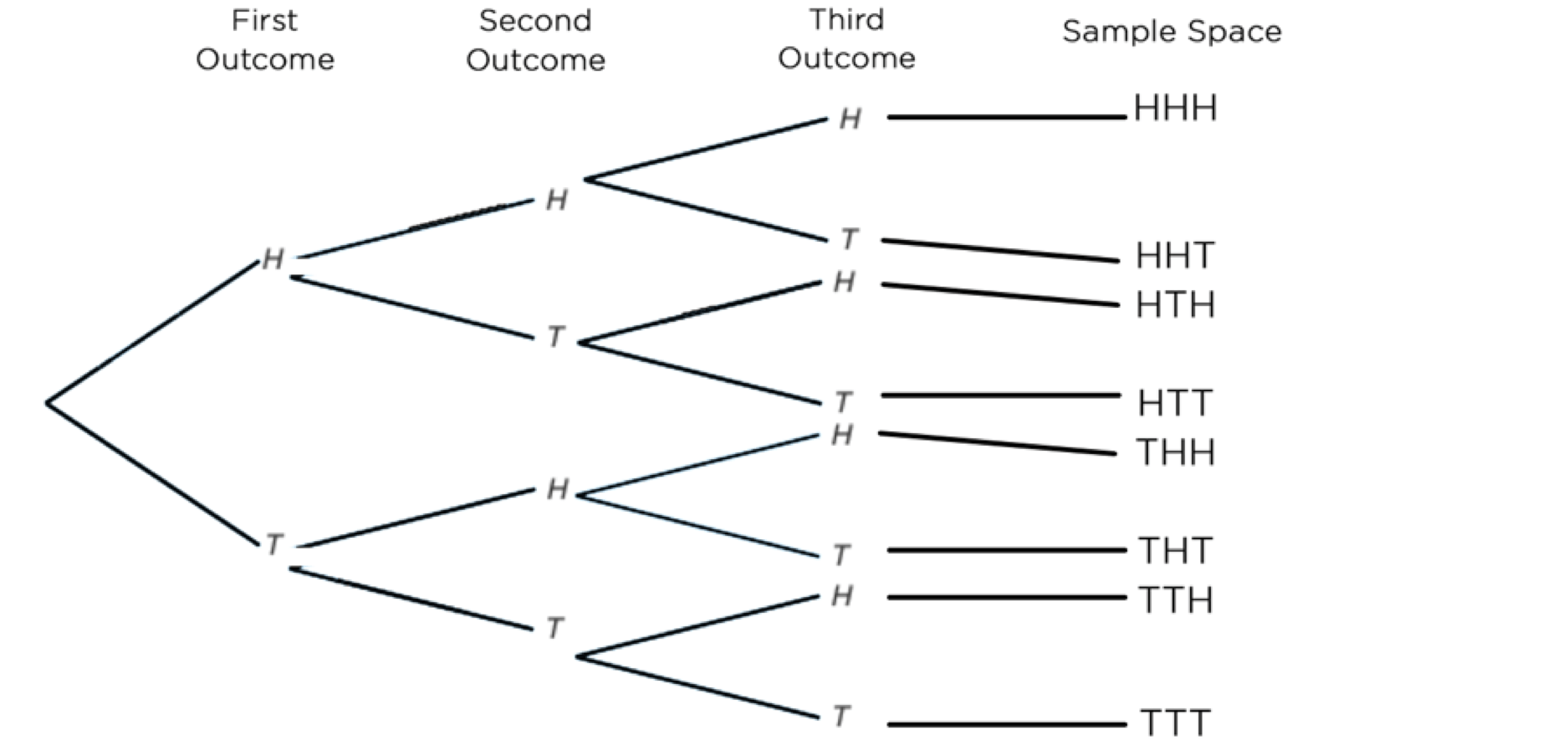
On the GRE, it is always helpful to list the elements of the sample space systematically by means of a tree diagram. For example, an experiment consists of flipping a coin thrice.
The figure below shows the various paths that give the distinct elements of the sample space. Starting with the top left branch and moving to the right along the first path, we get the sample point HHH, indicating the possibility that heads occur on three successive flips of the coin. Likewise, the sample point TTH indicates the possibility that the coin will show a tail on the first toss, followed by another tail on the second toss and then a head on the third toss. By proceeding along all paths, we see that the sample space is
S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}.
Another example (this one is from an official GRE guide question by ETS)
Example A: Of the 700 members of a certain organization, 120 are lawyers. Two members of the organization will be selected at random. Which of the following is closest to the probability that neither of the members selected will be a lawyer.
Now, we will solve this question later on in our discussion, but for the time being, let’s try to list out the sample space. So an experiment, in this case, consists of selecting two members from an organization. Therefore the possible elements of the sample space are LL, LN, NL, and NN, where L and N correspond to lawyers and not a lawyer, respectively.
Another example from the official GRE questions
Example B: A box contains 5 orange disks, 4 red disks, and 1 blue disk. You are to select two disks at random and without replacement from the box. What is the probability that one of the disks selected is blue?
Again, we will solve this question later on in our discussion, but for the time being, let’s try to list out the sample space. So an experiment, in this case, consists of selecting two disks. Therefore the possible elements of the sample space are OO, RR, OB, BO, OR, RO, RB, and BR where O, R, and B correspond to orange, red and blue, respectively.
Events
For any given experiment, the GRE may ask you about the occurrence of certain events rather than in the occurrence of a specific element in the sample space. For instance, in example A above, the GRE is asking you only about a specific element in the sample space i.e. neither of the two are lawyers (NN). However, in example B above, the GRE is interested about the occurrence of certain events. This will occur if the outcome is an element of the subset = {OB, BO, RB, BR} of the sample space OO, RR, OB, BO, OR, RO, RB, and BR. Therefore an event is a subset of the sample space.
Complement
Consider an experiment in which the smoking habit of employees is recorded. A possible sample space might classify an employee as a chain smoker, occasional smoker or a nonsmoker. Let the subset of smokers be some event. Then all the nonsmokers correspond to a different event, which is also a subset of this sample space. This subset is called the complement of the set of smokers.
The complement of an event A of sample space S is the subset of all elements of S that are not in A. Generally GRE denotes the complement of A by the symbol A`.
For example, consider a sample space S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT} where H, T represent heads and tails respectively. Let A = {HHH, HHT, HTH}. Then complement of A will be {HTT, THH, THT, TTH, TTT}.
Intersection
Consider the sample space S = {3, 6, 9, 12, 15, 20, 21, 23}.
Let A be an event that the number is divisible by 6, hence A= {6, 12}. Let event B be an event that the number is divisible by 3, hence B = {3, 6, 9, 12, 15, 21}
Now both events A and B will occur if the outcome is an element of the subset {6, 12}, which is just the intersection of A and B.
On the GRE, the intersection of two events A and B, is the subset (event) containing common elements to A and B.
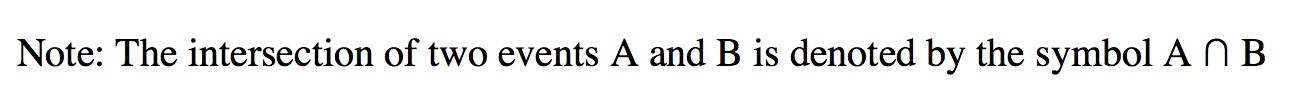
Mutually Exclusive
In another example, if we say that A is the event that a person selected in a class is a female and B is the event that a person selected in the class is a male. Then A intersection B is the event of all female students in the classroom who are also males, which is clearly not possible 🙂 (at least not on the GRE). Therefore A intersection B = 0.
Two events A and B are mutually exclusive, or disjoint, if A intersection B = 0, that is if A and B have no elements in common.
Union
Seldom, GRE asks about the occurrence of at least one of two events associated with an experiment. Thus, in the following example, let events A and B be defined as follows:
A= {2, 6, 12}, B = {3, 6, 9, 12, 15, 21}
The GRE might be interested in either A or B or both occurring. This event is called the union of A and B. It will occur if the outcome is an element of the subset {2, 3, 6, 9, 12, 15, 21}.
The union of the two events A and B, is the event that contains all elements that belong to A or B or both.
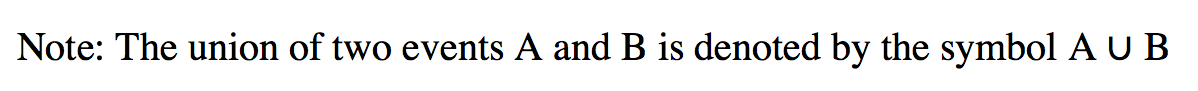
In another example, let X be defined the event that a student is under 30 years old. Let Y be the event that a student is a high school graduate. Then the event X union Y is the set of all students who are either under 30 years old or are high school graduates or both. In other words, it contains all students except those who are neither under 30 nor high school graduates. Or we can also say that the complement of X union Y contains all above 30 years old people who are not high school graduates.
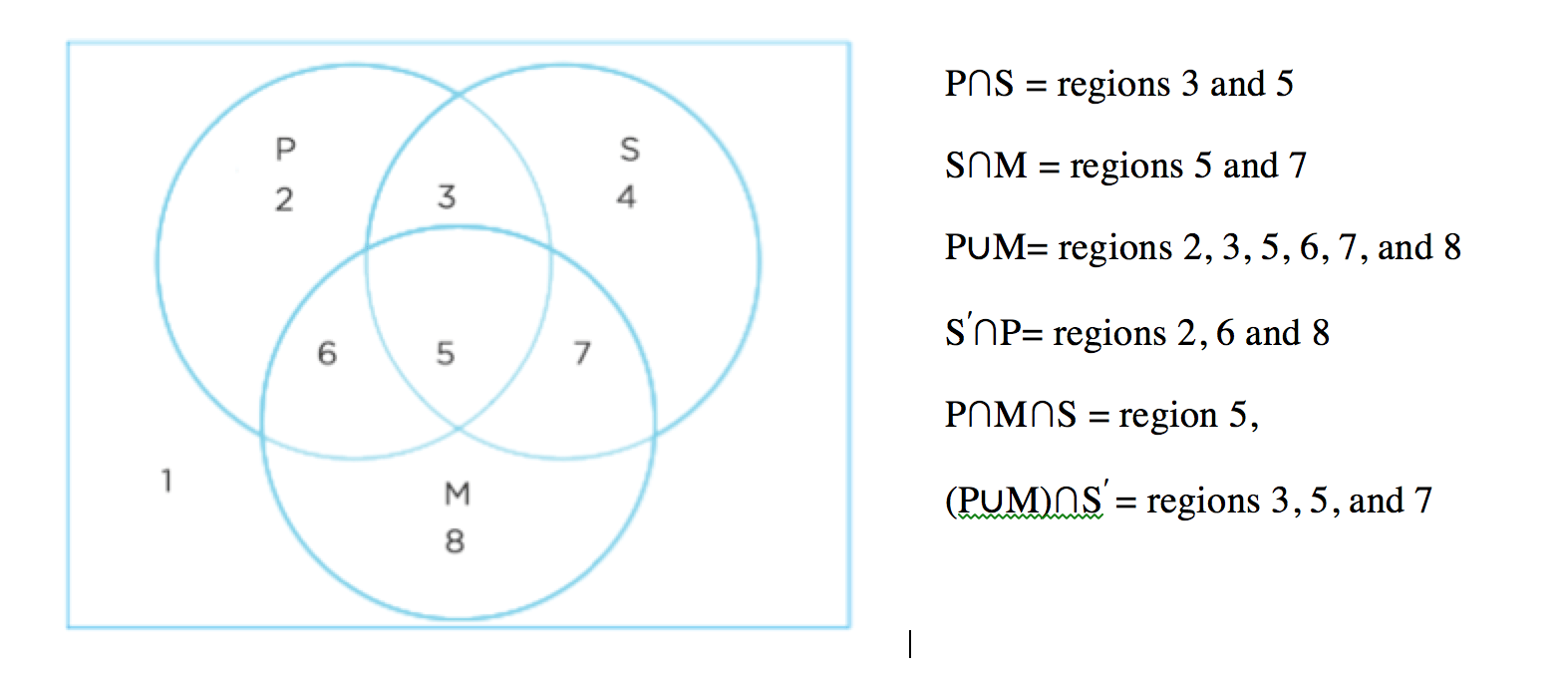
Venn Diagrams
On the GRE, events and the corresponding sample space can also be sometimes illustrated graphically through a Venn diagram. In a Venn diagram, the rectangle represents the sample space and the circles represent the events. For example, the Venn diagram below shows different intersection and/or unions of events.
2. Probability of an Event
The likelihood of the occurrence of an event is calculated by means of probabilities, ranging from 0 to 1, inclusive. To every element in the sample space, we assign a probability such that the sum of all probabilities is 1. If we have reason to believe that a certain sample point is quite likely to occur when the experiment is conducted, the probability assigned should be close to 1. On the other hand, 0 is the probability assigned to a sample point that is not likely to occur.
In many experiments, such as tossing a coin or a die, all the sample points have the same chance of occurring and are assigned equal probabilities. For points outside the sample space, that is, for simple events that cannot possibly occur, we assign a probability of 0.
To find the probability of an event A, we sum all the probabilities assigned to the sample points in A. This sum is called the probability of A and P(A) is used to denote it.
Hence, P(A) is between 0 and 1, inclusive 1, and P(S) = 1.
Furthermore, if A1, A2, A3, … is a sequence of mutually exclusive events, then
P (A1 union A2 union A3 · · · ) = P (A1 ) + P (A2 ) + P (A3 ) + · · · .
Example 2a:
You toss a coin twice. What is the probability that at least 1 head occurs?
Solution 2a: The sample space for this experiment is S = {HH,HT,TH,TT}.
If the coin is unbiased, each of these outcomes is equally likely to occur. Therefore, we assign a probability of w to each sample point. Then 4w = 1, or w = 1/4. If A represents the event of at least 1 head occurring, then
A = {HH,HT,TH} and P(A) = 1/4+ 1/4 + 1/4= 3/4 (Answer)
Example 2b:
Suppose that there is a 6-sided die that is weighted in such a way that each time the die is rolled, the probabilities of rolling any of the numbers from 1 to 5 are all equal, but the probability of rolling a 6 is twice the probability of rolling a 1. When you roll the die once, the 6 outcomes are not equally likely. What are the probabilities of the 6 outcomes?
Solution 2b: The sample space is S = {1, 2, 3, 4, 5, 6}. We assign a probability of w to each outcome from 1 through 5 but and a probability of 2w to the last outcome, which is 6. Since the sum of the probabilities must be 1, we have 7w = 1 or w = 1/7. Hence, the probability of each outcome from 1 through 5 is 1/7 and the probability of rolling a 6 is 2/7. (Answer)
Example 2c:
In example 2b, let A be the event that an even number turns up and let B be the event that a number divisible by 3 occurs. Find P (A union B) and P (A intersection B).
Solution 2c: For the events A = {2,4,6} and B = {3,6}, we have A union B = {2, 3, 4, 6} and A intersection B = {6}.
By assigning a probability of 1/7 to each number from 1 through 5 and 2/7 to 6, we have P (A union B) = 1/7 + 1/7 + 1/7 + 2/7 = 5/7 and P (A intersection B) = 2/7. (Answer)
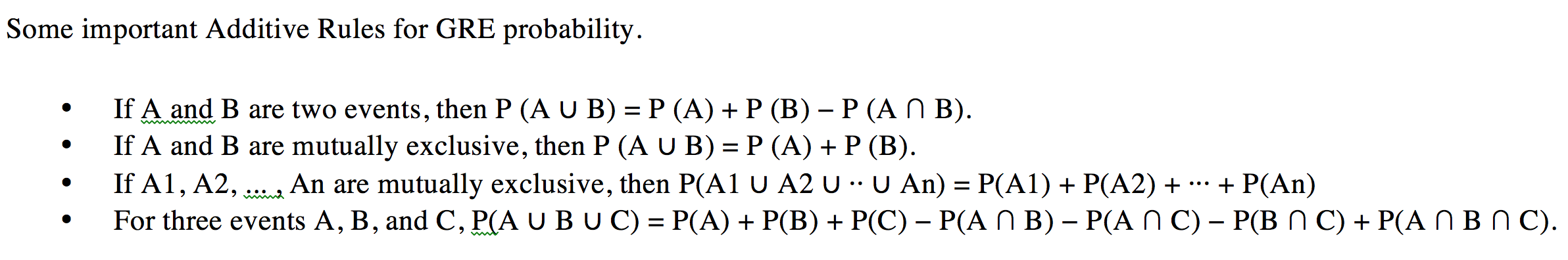
Example 2d:
Aaron is selecting the courses that he is going to study the next semester. After going through the course list, he assesses that his probability of studying French is 0.8 and that his probability of studying Spanish is 0.6. If he believes that the probability that he will study both French and Spanish is 0.5, what is the probability that he will study at least one of the two courses?
Solution 2d: Using the additive rule, we have P (A union B) = P (A) + P (B) – P (A intersection B) = 0.8 + 0.6 – 0.5 = 0.9. (Answer)
Note: If A and A` are complementary events, then P(A) + P(A`) = 1.
Example 2e:
If the probabilities that a person will take 1, 2, 3, 4, 5, 6 or more hours to finish a task are respectively, 0.12, 0.19, 0.28, 0.24, 0.10, and 0.07, what is the probability that it will take him at least 2 hours to finish the task?
Solution 2e: Let E be the event that it takes at least 2 hours to finish the task. Now, P (E) = 1 – P (E`), where E` is the event that it takes fewer than 2 hours to finish the task. Since
P(E`) = 0.12, it follows that P(E) = 1 – 0.12 = 0.88. (Answer)
Example 2f:
Suppose the margin of error of an industrial machine, while producing a product, is 12 centimeters ± 1 centimeter. Moreover, the probability of randomly producing a product with length exceeding 13 centimeters is equal to the probability of producing a product with length smaller than 11 centimeters. Also, the probability that there will be no error is 0.85. What is the probability that a product will exceed the error limit?
Solution 2f: Let A be the event that a product falls within the error limits. Then
P (A) = 0.85 and 1 – P(A) = 0.15, which denotes that the product either exceeded or fell behind the required range. Since the probability of a product being larger than 13 is the same as the probability of a product being smaller than 11, hence 0.15/2 = 0.075. 0.075 is the probability that a product will exceed the error limit. (Answer)
3. Dependent & Independent Events on GRE
Independent: Two events A and B are said to be independent if the occurrence of either event does not affect the occurrence of the other.
If two events A and B are independent, then P (both A and B occur) = P(A) * P(B).
For example, if a dice is rolled twice, the event A of rolling a 6 on the first roll and the event B of rolling a 6 on the second roll are independent. Therefore the probability of rolling a 6 on both rolls is P(A) * P(B)= 1/6 * 1/6 = 1/36. Event A restricts only the first roll—to a 6—having no effect on the second roll; and vice versa.
In another example, if a dice is rolled once, let A be the event of rolling a 6 and let B be the event of rolling an even number. These events are not independent. This is because rolling a 6 makes sure that the event of rolling an even number occurs. Note that P (both A and B occurring) not equal to P(A)*P(B), since P(A and B) = P(A) = 1/6 and P(A)*P(B) = 1/6*3/6 = 1/12.
Example 3a:
We have a box containing 20 items, of which 5 are defective. If 2 items are selected at random and without replacing the first, what is the probability that both items are defective?
Solution 3a: We shall let A be the event that the first item is defective and B the event that the second item is defective; then we interpret A intersection B as the event that A occurs and then B occurs after A has occurred. Note that these two events are not independent, since the occurrence of event A changes the sample space for event B.
The probability of first removing a defective item is 5/20 (1/4); then the probability of removing a second defective item from the remaining 4 is 4/19. Hence,
P(A intersection B) = 5/20 * 4/19 = 1/19. (Answer)
Example 3b:
Let’s reconsider example 3a as follows: We have a box containing 20 items, of which 5 are defective. If 2 items are selected at random and with replacement, what is the probability that both items are defective?
Solution 3b: We shall let A be the event that the first item is defective and B the event that the second item is defective; then we interpret A intersection B as the event that A occurs and then B occurs after A has occurred. Note that these two events are now independent, since the occurrence of event A does not change the sample space for event B.
The probability of first removing a defective item is 5/20; the probability of removing a second defective item from the remaining also remains 5/20. Hence,
P(A intersection B) = 5/20 * 5/20 = 1/16 (Answer)
* This is an exhaustive purview of probability topics, concepts, formulas and rules that are tested on the GRE. You do not need to consult any advanced probability books to prepare for GRE probability. The above article will serve the purpose on GRE probability.
For any confusion or if you need more clarification on any concept/example discussed above, please feel free to leave a question in the comment box below.
